Research
Throughout my research career, I have been fascinated by the power of mathematics to reveal hidden patterns in biological systems. My research lies at the intersection of quantitative modeling and the life sciences, where I develop and use mathematical frameworks to understand complex phenomena, ranging from cellular dynamics (on the microscopic scale) to population behavior (on the macroscopic scale). The main factor that drives me is not just the elegance of equations and mathematical formulae, but their ability to make sense of the living world.
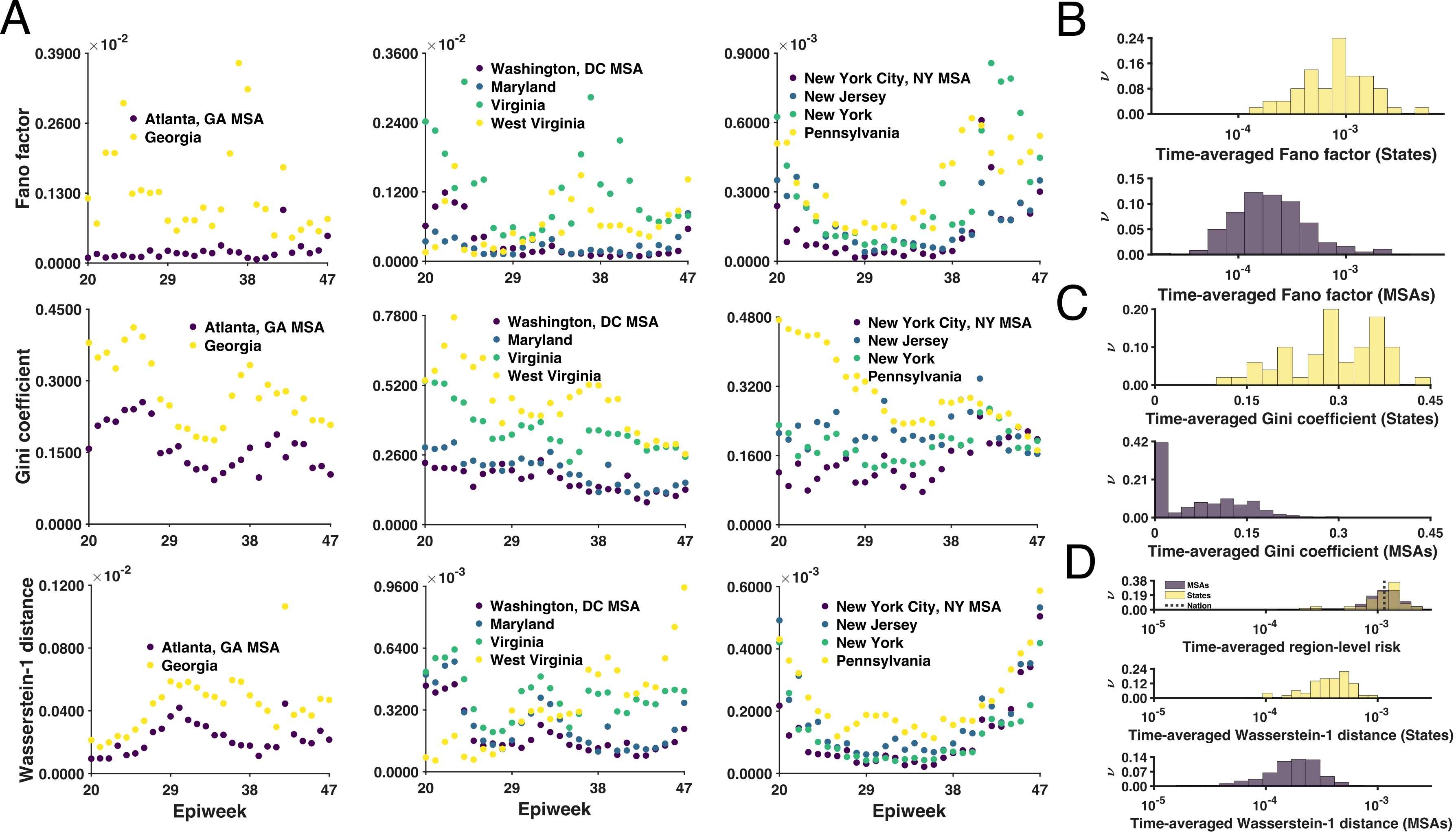
Differential contagiousness of respiratory disease across the United States
The initial contagiousness of a communicable disease within a given population is quantified by the basic reproduction number. This number depends on both pathogen and population properties. On the basis of compartmental models that reproduce Coronavirus Disease 2019 (COVID-19) surveillance data, we used Bayesian inference and the next-generation matrix approach to estimate region-specific basic reproduction number values for 280 of 384 metropolitan statistical areas (MSAs) in the United States (US), which account for 95% of the US population living in urban areas and 82% of the total population. We focused on MSA populations after finding that these populations were more uniformly impacted by COVID-19 than state populations. Our maximum a posteriori (MAP) estimates for the basic reproduction number range from 1.9 to 7.7 and quantify the relative susceptibilities of regional populations to spread of respiratory diseases.
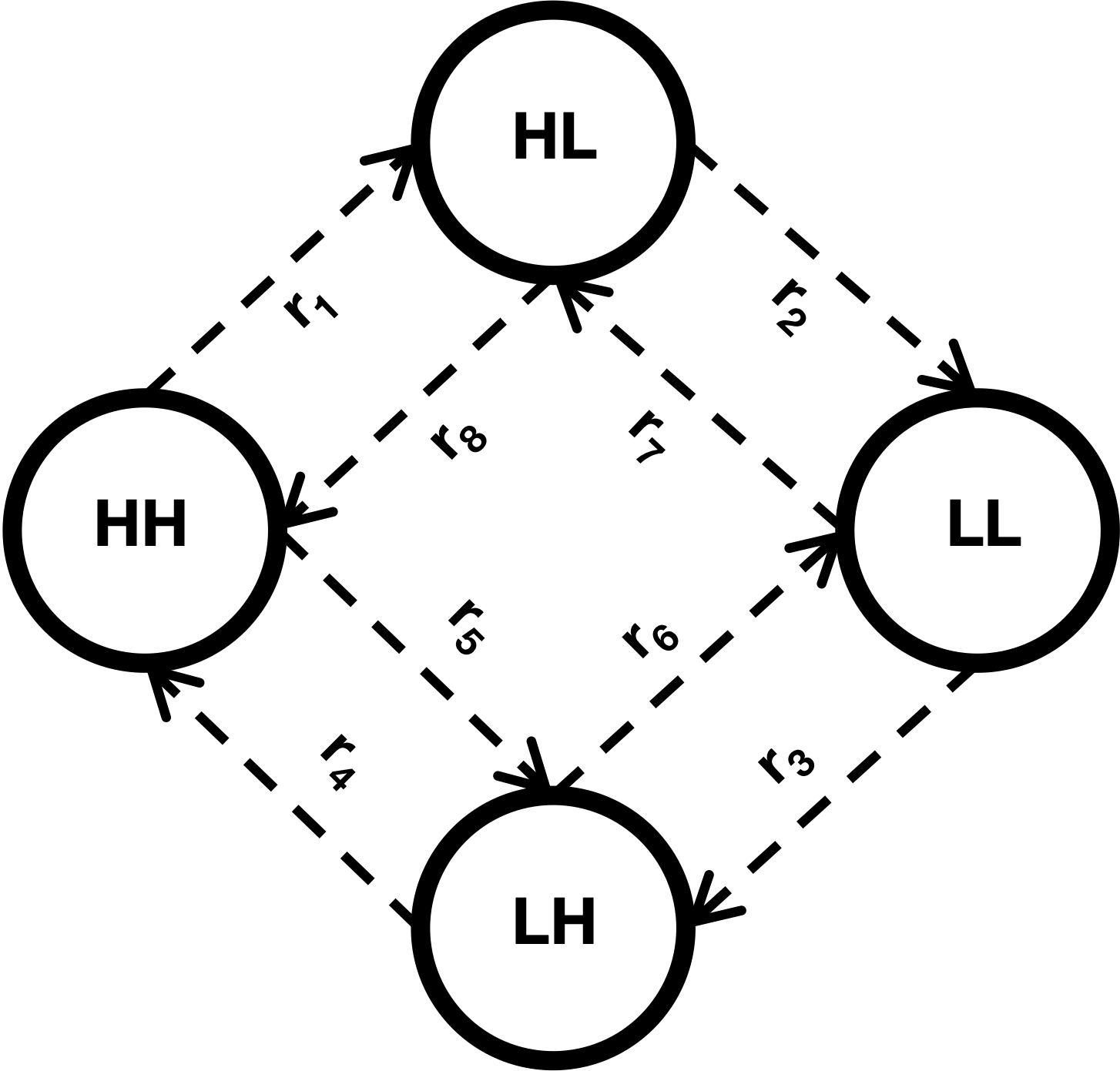
The role of stochasticity in noise-induced tipping point cascades: a master equation approach
Tipping points have been shown to be ubiquitous, both in models and empirically in a range of physical and biological systems. The question of how tipping points cascade through systems has been less explored and is an important one. A study of noise-induced tipping, in particular, could provide key insights into tipping cascades. Here, I consider a specific example of a simple model system that could have cascading tipping points. This model consists of two interacting populations with underlying Allee effects and stochastic dynamics, in separate patches connected by dispersal, which can generate bistability. From an ecological standpoint, I look for rescue effects whereby one population can prevent the collapse of a second population. As a way to investigate the stochastic dynamics, I use an individual-based modeling approach rooted in chemical reaction network theory. Then, using continuous-time Markov chains and the theory of first passage times, I essentially approximate, or emulate, the original high-dimensional model by a Markov chain with just three states, where each state corresponds to a combination of population thresholds. Analysis of this reduced model shows when the system is likely to recover, as well as when tipping cascades through the whole system.
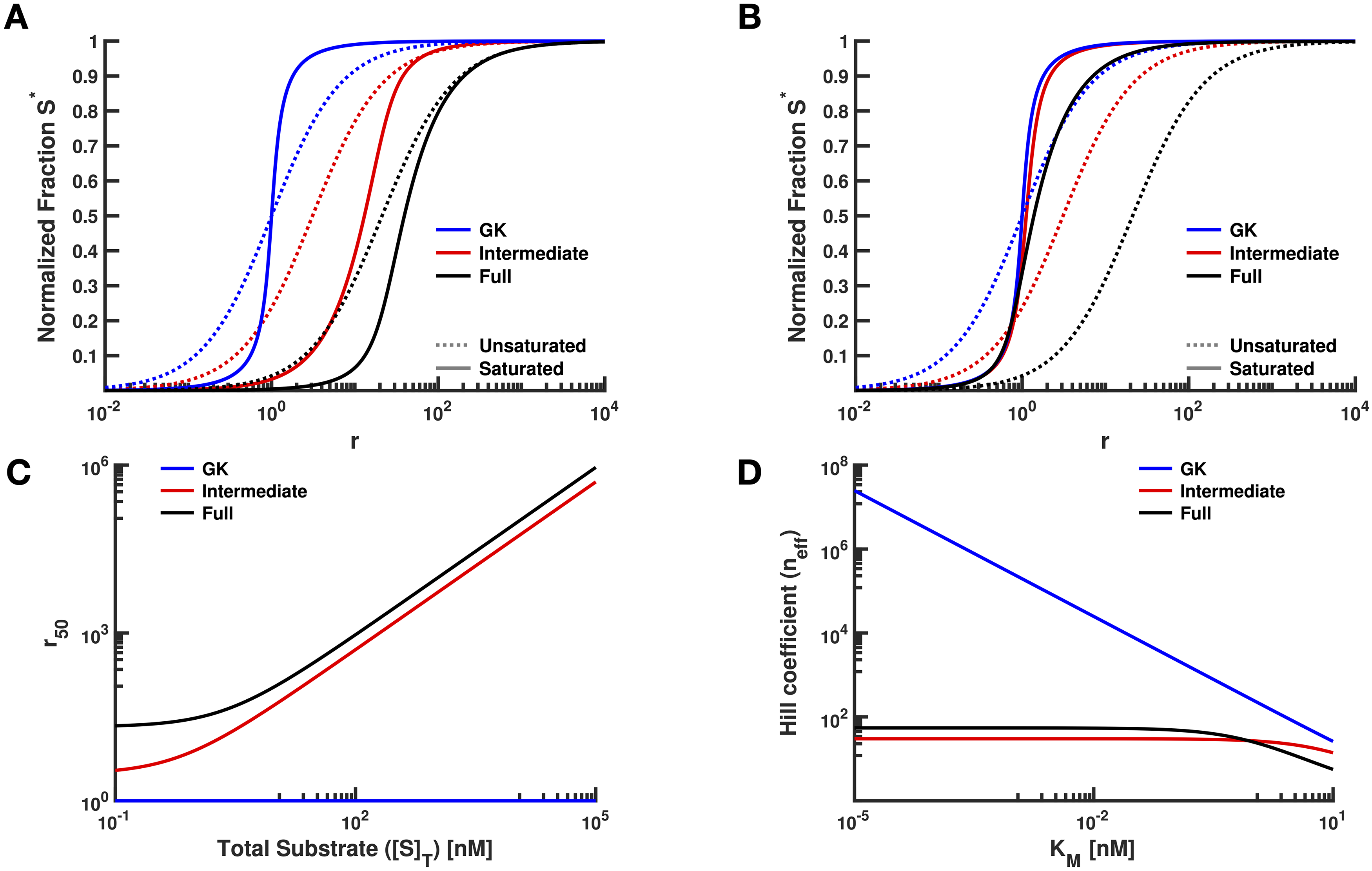
Crosstalk and ultrasensitivity in protein degradation pathways
Previous work has shown that substrates of Post-Translational Modification (PTM) cycles can have coupled responses if those substrates share enzymes. This implies that modifications leading to substrate degradation (e.g. ubiquitylation by an E3 ligase) could introduce coupling in concentrations of substrates sharing a ligase. Using mathematical models, we found adding protein turnover to a PTM cycle diminishes both sensitivity and ultrasensitivity, particularly in models admitting long ubiquitin chains. We also found that proteins sharing an E3 ligase can indeed have coupled changes in both expression and sensitivity to signals. These results imply that accounting for crosstalk in protein degradation networks is crucial for the interpretation of results from a wide variety of common experimental perturbations to living systems.
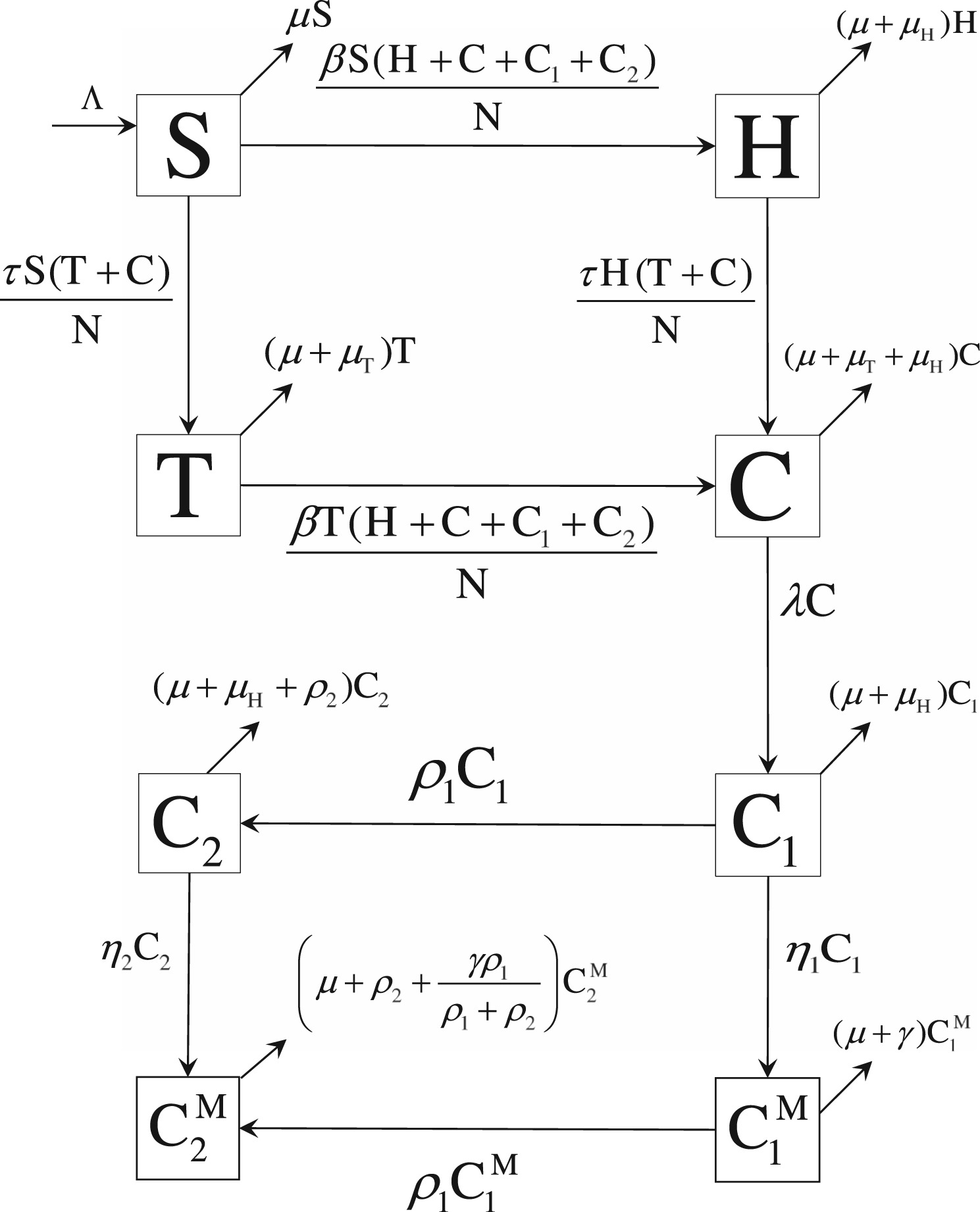
HIV–TB co-infection treatment: Modeling and optimal control theory perspectives
An important question, of whether the initiation of HIV treatment during ongoing TB treatment for HIV–TB co-infected individuals is appropriate, still remains unanswered; initiating HIV treatment at or soon after the start of the TB treatment course has some advantages including fewer HIV-related deaths and a lower risk of HIV transmission as well as some disadvantages including occurrence of Immune Reconstitution Inflammatory Syndrome (IRIS) due to a high pill burden. In this study, we developed a mathematical model to explore the effects of early and late HIV treatment, during the TB treatment course, on new HIV infections, HIV-related deaths, and IRIS cases. Mathematical analyses of our model indicate that co-infection treatment programs alone cannot eradicate the diseases; additional interventions and/or treatments targeting individuals infected with a single disease are necessary for successful disease eradication. Numerical computations of the model solution demonstrate that outcomes of the treatment programs aiming to reduce the total burden of this co-infection depend highly on both the strength and initiation timing of antiretroviral therapy (ART). Based on our model, we also formulated an optimal control problem and solved it using Pontryagin’s Maximum Principle and an efficient numerical iterative method. Our numerical results of an optimal HIV–TB treatment protocol that yields a minimum burden from this co-infection indicates that each of the new HIV infections, HIV-related deaths and IRIS cases is important for achieving optimal benefits from the co-infection treatment programs.